Swiss Tables:A Modern, High-Performance Hash Table
Swiss Table is a high-performance hash table design introduced by Google engineers in 2017. It has since inspired many standard-library implementations across languages, including:
- Go 1.24 ships its map with this design (up to 60% faster)
- Rust’s standard HashMap has also moved from Robin Hood hashing to a Swiss Table-inspired layout.
- Datadog reported as much as 70% memory savings after migrating to Swiss Table
Open Addressing, Briefly
An open addressing hash table is one of the implementation methods for hash tables. Unlike separate chaining — which uses external data structures such as linked lists or trees — open addressing implements the entire hash table as a single contiguous array.
In an open addressing hash table, when a hash collision occurs, the algorithm probes other empty slots within the table to find a location where the key can be placed.
Typical examples of open addressing strategies include:
- Linear Probing: Move one slot (
j) at a time from the original hash position (i) - Quadratic Probing: Move
j²slots from the original hash position (i)

Linear probing animation from: https://dev.to/huizhou92/swisstable-a-high-performance-hash-table-implementation-1knc
Control Bytes
Each slot carries a 1-byte metadata called a control byte that speeds up lookups and inserts. Control bytes help you quickly spot empty slots, and the short H2 fingerprint gives fast first-pass matches so each probe does less work.

from: CppCon 2017 — Matt Kulukundis, Designing a Fast, Efficient, Cache-friendly Hash Table, Step by Step
Control byte states:
| State | Value | Meaning |
|---|---|---|
| Empty | 0x80 | Slot is empty |
| Deleted | 0xFE | Slot was deleted |
| Full | 0x00–0x7F | Occupied; stores H2 (7-bit fingerprint) |
Grouped SIMD Scans
Modern hash table implementations actively leverage modern hardware to maximize performance. They often use SIMD vector operations to optimize bit operations on control bytes.
The control byte array is processed in chunks the size of the SIMD register VL (e.g., 128 bits). This chunk is called a control byte group (Group). It is not a physically separate structure—just a logical processing unit.
Typical bit split (assuming 64-bit hash):
H1: upper 57 bits → group indexH2: lower 7 bits → fingerprint in the control byte
For 32-bit hashes, a split like 25/7 also works.
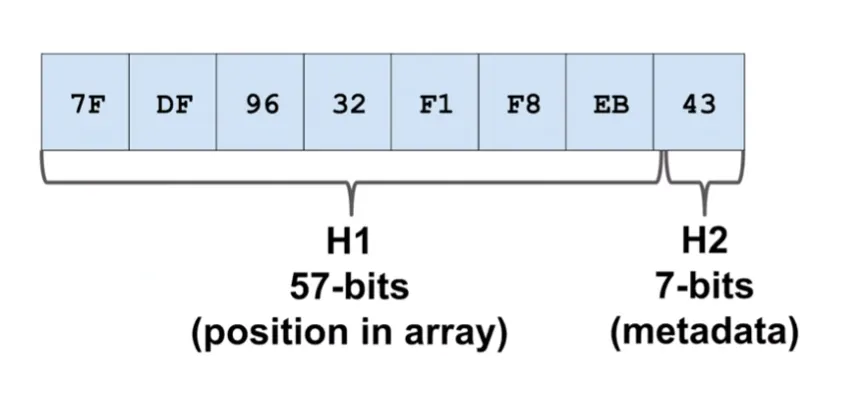
image from: Abseil Swiss Tables Design Notes
How it works:
- Hash the key and split into
H1andH2. - Use
H1to pick the starting control-byte group. - SIMD-compare the group’s control bytes with
H2(the fingerprint). - On a match, confirm the actual key; stop if an
Emptyis found. - Otherwise, advance to the next group and repeat.
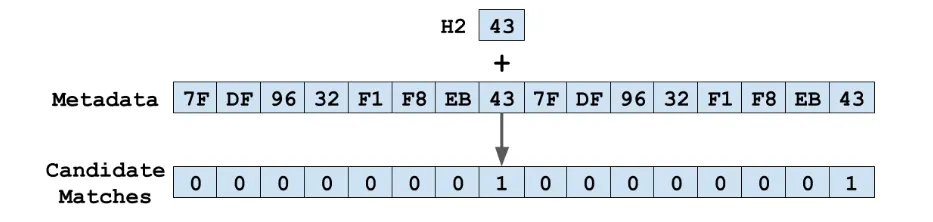
image from: Abseil Swiss Tables Design Notes